El crecimiento del número de casos del COVID-19 en Chile alertan de un momento determinante de la pandemia, los modelos matemáticos siguen siendo una de las claves principales para predecir lo que se aproxima, y lo más importante entregar variados escenarios que los estados deben considerar en la toma de decisiones. Analizaremos dos indicadores de la pandemia modelados según los datos reales de Chile en dos momentos cercanos del pico del virus. Estos son el comportamiento de la incidencia de casos y sus posibles proyecciones para los días siguientes y el segundo el importante factor número reproductivo efectivo (Rt); que es el número promedio de infecciosos generados por un individuo infectado en la población en cualquier día. La segunda métrica es de suma importancia para estimar el control final de la pandemia, ya que su tendencia a cero elimina la reproducción del virus.
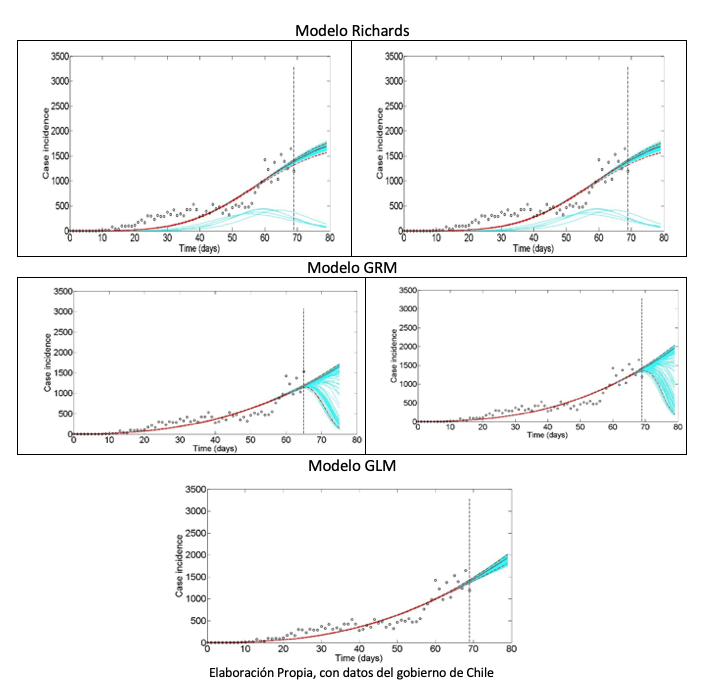
Para el primer indicador se usan tres métodos de los llamados modelos fenomenológicos (modelos no lineales), estos modelos no tienen en cuenta los mecanismos de transmisión de la enfermedad, pero tienen la ventaja que solo con la información de los casos anteriores, pueden dar pronósticos del número de casos, de cuantos se van a infectar al final de la epidemia, donde será el pico, u otros. Los modelos fenomenológicos utilizan pocos parámetros, hacen suposiciones más sencillas, y son probables a dar estimaciones más robustas cuando son aplicados en contextos con datos muy limitados
La modelación de datos es realizada por los modelos fenomenológicos más utilizados, para las enfermedades infecciosas; el modelo de Richards (RM) (1959), el modelo logístico generalizado (GLM) y el modelo de Richards generalizado (GRM) (1969), el primero de ellos es un modelo de crecimiento que considera cuatro variables, uno de sus parámetros permite modelar las curvas con mayor precisión, sin embargo, es criticado ya que este parámetro no tiene significado biológico. El segundo, el GLM es una función usada en diversos modelos de crecimiento en poblaciones, propagación de pandemias u otros; esta función es una generalización flexible de las regresiones simples, con distribución de errores distintos a la distribución normal y el último es una generalización de los dos modelos anteriores.
Los análisis estadísticos de los tres modelos de nuevos casos, en dos momentos del virus (8 y 12 de mayo), son realizadas por a través del sistema MATLAB (sistema de cómputo numérico), siendo la línea discontinua, el día real de la propagación. Los tres modelos apuntan hacia un mismo horizonte, la curva de crecimiento de los casos nuevos entró en su crecimiento exponencial, la curva más probable predice cerca de hasta 4000 casos en los próximos días y los casos pueden crecer de manera alarmante. Sólo medidas gubernamentales estrictas de distanciamiento social y conciencia social del fenómeno, pueden hacer que lo que sigue tienda a la situación más favorable (líneas celestes de los modelos), de no ser así la consecuencia inmediata será el colapso completo del sistema de salud, como ha pasado en variados lugares del mundo, con una cantidad de muertes en el mismo crecimiento exponencial.
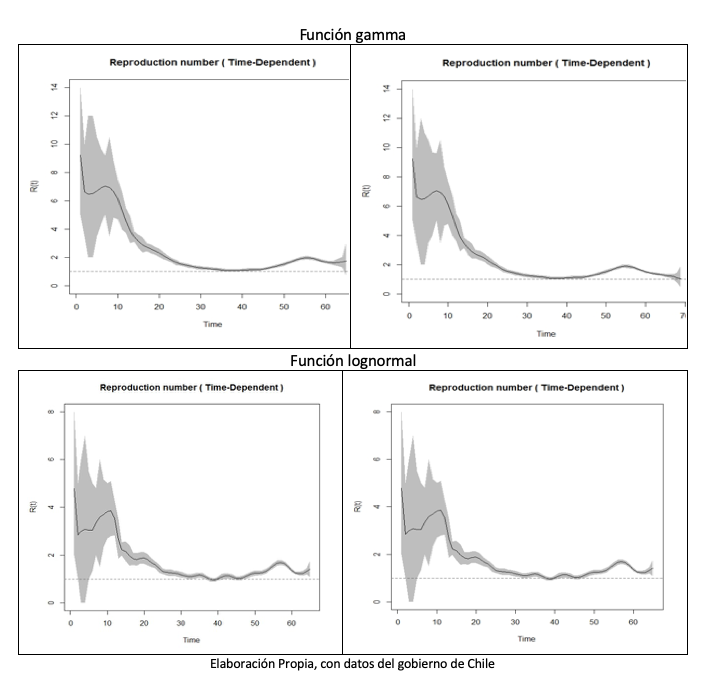
Para el modelamiento del segundo factor, el número reproductivo efectivo (Rt); se usan dos distribuciones de probabilidad para el tiempo de generación o el intervalo serial, las distribuciones gamma y lognormal. Para ambas distribuciones el indicador se ha mantenido estable, cercano a 1 con leve crecimiento en algunos períodos de tiempo, este indicador es de gran importancia en casos de pandemias, dado que su cercanía a cero puede asegurar la cercanía final de la pandemia, situación que no ha ocurrido. Dado el posible crecimiento de nuevos casos, y sus posibles tendencias analizadas es de mucha importancia observar el comportamiento futuro de este indicador.
Los análisis de ambos indicadores nos ponen en dos escenarios, el primero el del avance de la enfermedad según lo hacen los virus del tipo analizado, o sea el crecimiento exponencial de casos nuevos, que podemos verlos aumentar de manera multiplicativa en muy pocos días, con las consecuencias vividas en otras partes del mundo. El segundo escenario “es hacer aplanar la curva”, y eso solo se logra con medidas más estrictas de distanciamiento y aumentar el número de testeos diarios. Las funciones exponenciales en el momento de crecimiento no aceptan posiciones intermedias.
En el país se han establecidos políticas públicas aceptables para contener la epidemia Covid-19: aislamiento, cuarentenas, distanciamiento social, reordenamiento laboral, restricciones de viajes, etc. A pesar de estas políticas el número de casos sigue aumentando y el país necesita tomar decisiones sobre diferentes recursos para lograr controlar la epidemia. La modelación matemática habla y dice el camino a seguir, es el último momento de entenderlo por todos, es la hora de pensar en el bien común.
Alexis Matheu, Carlos Sebrango
Centro de Investigación Institucional
Análisis Institucional 2020
Universidad Bernardo O’Higgins